The REM Algorithm¶
If the Gaussian components in a GMM are well separated, then the density peaks exactly match the Guassian means; if the components overlap a bit, then the density peaks would include but not limited to the Guassian means. This motivates us to apply, e.g., the Gaussian kernel, to approximately locate the density peaks, within which to pinpoint the Guassian means. However, we can do better (from the algorithm point of view), if we replace the estimated density peaks with the exemplars from the data. An exemplar here is an observed unit in the vicinity of a density peak, and thus can well represent the location of the density peak. (If two Gaussian components overlap a lot, their combined distribution could have only one density peak. However, this won't be an issue for clustering, as we can simply treat the combined distribution as one cluster/mixture component.)
The REM algorithm is an agglomerative hierarchical clustering method. It begins with every exemplar representing a cluster (center), and then iteratively prunes the exemplars that are not a Gaussian mean. There are mainly two reasons for pruning the exemplars:
(1) The density-peak finding method has tuning parameters, and it is unknowable whether each of the detected exemplars represents a unique density peak. In practice, the initial exemplar set inclues all possible exemplars, and hence there could be multiple exemplars associated with one density peak.
(2) The set of density peaks in a GMM is not in one-to-one correspondence with the set of Gaussian means: the number of peaks can be significantly larger than the number of mixture components. Therefore, even if the detected exemplars are unique density peaks, we still need to prune the exemplars to retaiin only the exemplars that represent the Gaussian means.
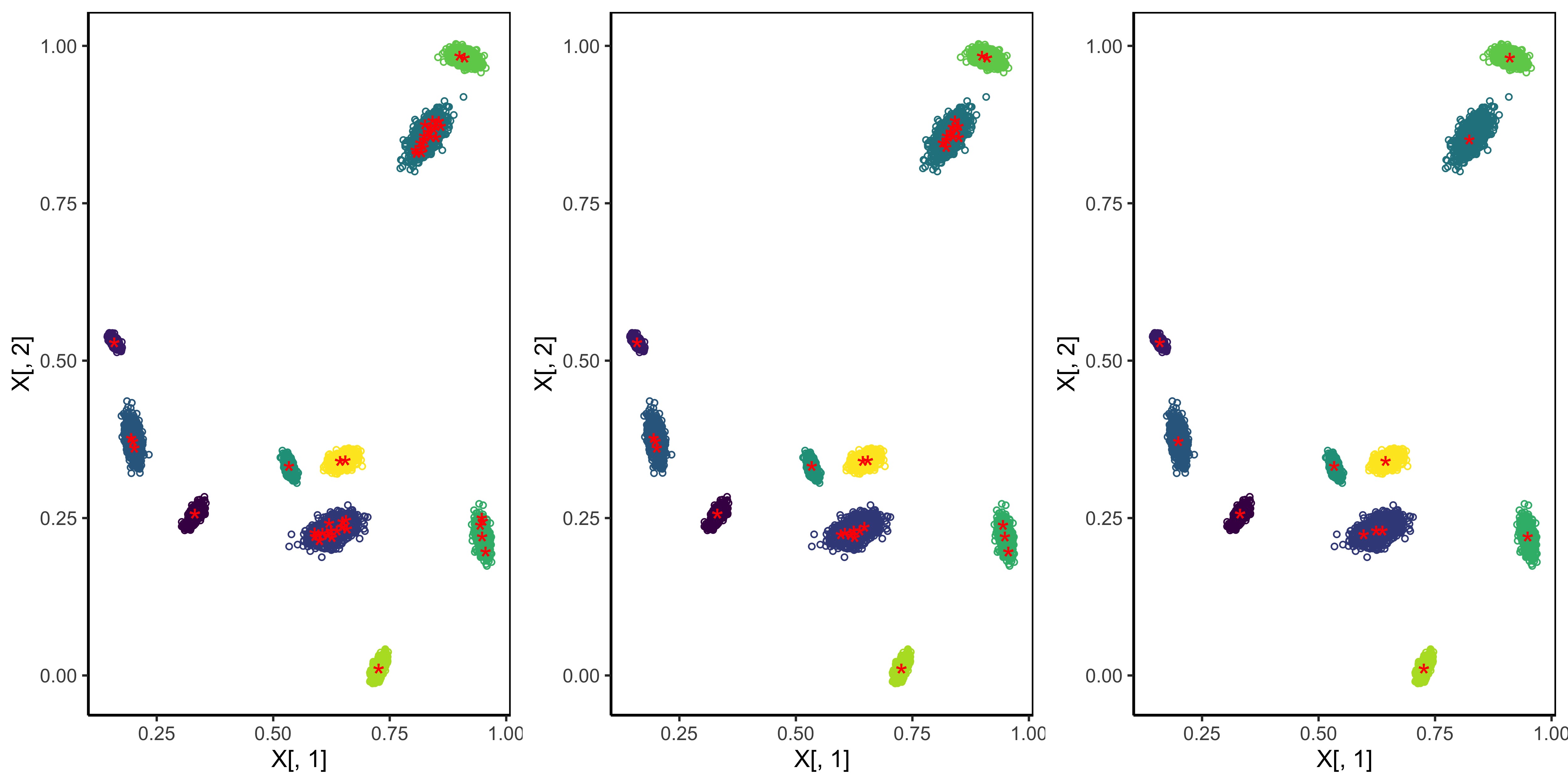
The figure below shows the detected exemplars (red stars) from the density-peak finding method with different settings of the tuning parameters. Well seperated Gaussian components are indicated by different colors. The density-peak finding method detects multiple exemplars for one density peak. An important feature of the REM algorithm is that it produces a decision graph that helps the user select all possible exemplars. We will explore this feature later.
The REM algorithm has two algorithmic blocks: the EM block and the pruning block. Given the updated data pool (the original data without the retained exemplars), the EM block operates as follows.
Input: The retained exemplars $\{\mathbf{e}_1, \ldots, \mathbf{e}_\kappa\}$ and the responsibilities $\{r_{ij}: i=1, \ldots, n, j=1, \ldots, \kappa\}$.
(1) Update the estimates: for $j=1, \ldots, \kappa$, \begin{align*} \pi_j=\frac{\sum_{i=1}^{n}r_{ij}}{n}, ~~~ \mathbf{\Sigma}_j=\frac{\sum_{i=1}^{n}r_{ij}(\mathbf{x}_i-\mathbf{e}_j)(\mathbf{x}_i-\mathbf{e}_j)^T}{\sum_{i=1}^{n}r_{ij}}. \end{align*}
(2) Compute the responsibilities: for $i=1, \ldots, n$ and $j=1, \ldots, \kappa$, \begin{equation*} r_{ij}=\frac{\pi_j\phi(\mathbf{x}_i; \mathbf{e}_j, \mathbf{\Sigma}_j)}{\sum_{v=1}^{\kappa}\pi_v \phi(\mathbf{x}_i; \mathbf{e}_v, \mathbf{\Sigma}_v)}. \end{equation*}
(3) Iterate steps 1 and 2 until convergence.
Output: The mixing proportions $\{\pi_1, \ldots, \pi_\kappa\}$ and the covariance matrices $\{\mathbf{\Sigma}_1, \ldots, \mathbf{\Sigma}_\kappa\}$.
We immediately notice that, in the EM block, the Gaussian means are fixed (at the given exemplars), and we only need to estimate the mixing proportions and covariance matrices. Since the exemplar set is disjoint from the dataset, the mean vectors will always differ from the data points, and therefore the iteration will never converge to a degenerate solution with a zero covariance matrix. The GMM density at convergence is \begin{equation*} f(\mathbf{x})=\sum_{j=1}^{\kappa}\pi_j \phi(\mathbf{x}; \mathbf{e}_j, \mathbf{\Sigma}_j). \end{equation*}
In the pruning block, we remove one exemplar from $\{\mathbf{e}_1, \ldots, \mathbf{e}_\kappa\}$. The idea is to introduce sparsity into the mixing proportion vector $\mathbf{\pi}$ such that, if $\pi_j=0$, then the exemplar $\mathbf{e}_j$ will be removed from the exemplar set (and put back into the data pool).
Input: The covariance matrices $\{\mathbf{\Sigma}_1, \ldots, \mathbf{\Sigma}_\kappa\}$.
(1) Calculate the weight vector $\mathbf{\delta}=(\delta_1, \ldots, \delta_\kappa)^T$: \begin{equation*} \delta_v = \max\left\{\Pr\left(\pi_v\phi(X; \mathbf{e}_v, \mathbf{\Sigma}_v) < \pi_j\phi(X; \mathbf{e}_j, \mathbf{\Sigma}_j) | X \sim N(\mathbf{e}_v, \mathbf{\Sigma}_v )\right): j = 1, \ldots, \kappa, j\neq v\right\},~~~~v=1, \ldots, \kappa. \end{equation*}
(2) Find the $\theta$ value such that the solution to the probem below, i.e., the responsibility matrix $\mathbf{R}=[r_{ij}]_{n\times\kappa}$, has exactly one column of zeros. \begin{align*} \min_{\mathbf{R}} ~~ \left\{\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^{\kappa} r_{ij}(\mathbf{x}_i-\mathbf{e}_j)^T\mathbf{\Sigma}_j^{-1}(\mathbf{x}_i-\mathbf{e}_j) + \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^{\kappa} r_{ij}\log \left(| \mathbf{\Sigma}_j|\right)+\theta\sum_{j=1}^{\kappa} \delta_j(\frac{1}{n}\sum_{i=1}^n r_{ij})\right\}, \\ \mbox{subject to}~~\sum_{j=1}^{\kappa} r_{ij}=1, ~~~i=1, \ldots, n. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{align*}
(3) Remove the exemplar $\mathbf{e}_j$ with $\sum_{i=1}^n r_{ij}=0$ and update $\kappa=\kappa-1$.
Output: The retained exemplars $\{\mathbf{e}_1, \ldots, \mathbf{e}_\kappa\}$ and the responsibilities $\{r_{ij}: i=1, \ldots, n, j=1, \ldots, \kappa\}$.
Both the weight vector $\mathbf{\delta}$ and the penalty function are well-motivatied. The original work Tobin et al. (2023) provides detailed explainations on them. In particular, the conditinal probability $\Pr\left(\pi_v\phi(X; \mathbf{e}_v, \mathbf{\Sigma}_v) < \pi_j\phi(X; \mathbf{e}_j, \mathbf{\Sigma}_j) | X \sim N(\mathbf{e}_v, \mathbf{\Sigma}_v )\right)$ is the likelihood that an instance from the vth mixture component is misclassified into the jth mixture component. Therefore, $\delta_v$ measures the overlapping degree of the vth mixture component w.r.t. the other mixture components. The pruning block is very efficient: (1) the algorithm complexity is linear, and (2) exemplars not representing Gaussian means are always pruned first.
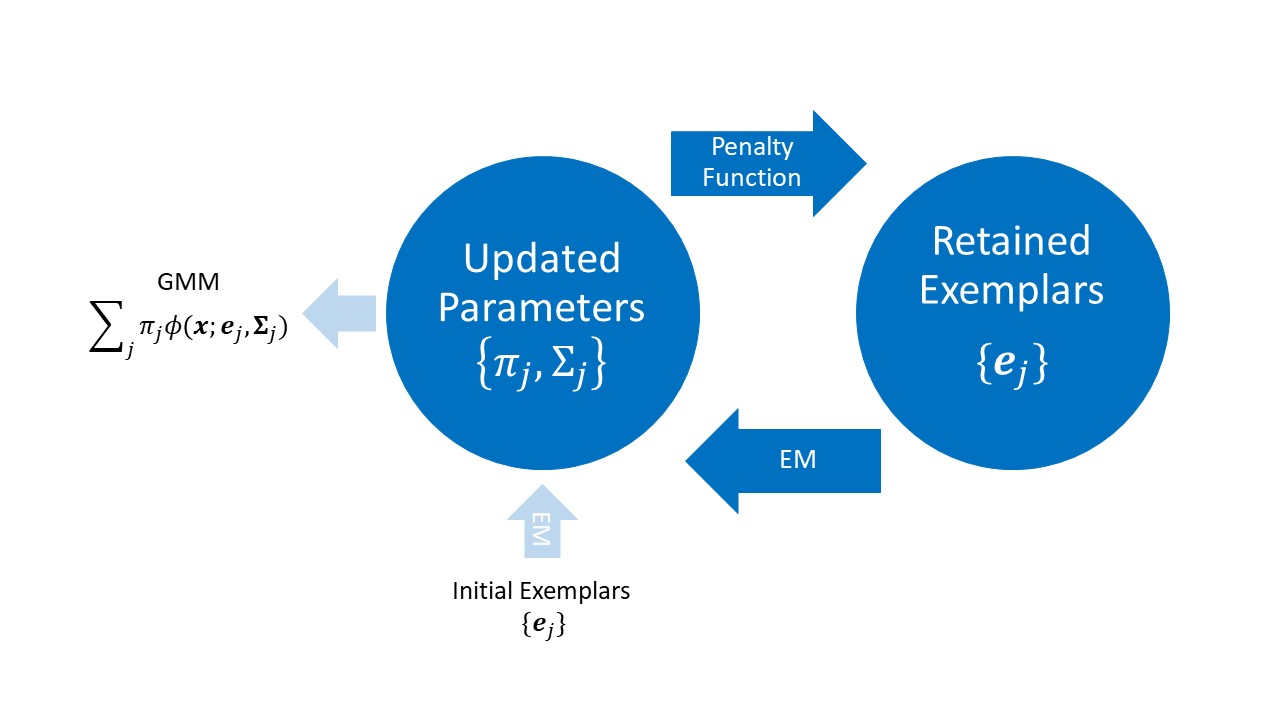
The flowchart below summarizes the REM algorithm. The blue left arrow "EM" means applying the EM block algorithm, and the blue right arrow "Penalty Function" means applying the pruning block algorithm. The loop produces a sequence of nested clusterings, and we pick the optimal clustering via the ICL criterion.